Navigation Buttons —
| Ideal Weight | Ideal Weight | The Paper | Appendix A | Appendix B | Appendix C | Appendix D |
|---|---|---|---|---|---|---|
| Imperial Units | Metric Units | Defining Ideal Bullet Weight | Math Model | Min. Wound | Depth and Vel. | Depth and Dia. |
Appendix C. Bullet Penetration Depth and Velocity for Expanding Bullets
Almost all of us hold to the well-established and scientifically proven notion that sectional density and velocity are critical parameters in determining depth of penetration. Indeed, penetration depth is proportional to the product of sectional density and velocity for solid and other projectiles that retain their initial shape through impact and penetration.

Figure C-1. Example expanded bullet. – 125 gr Nosler Partition® – The object pictured on the right does most of the penetration. We see that the expanded bullet is much shorter and possesses a lower sectional density. Photo courtesy of Steve Auger.
At first glance, however, expanding hunting bullets seem to be a different story. The bullet changes from a sleek aerodynamic projectile to a blunt slug resembling a low density sphere like what we see in Figure C-1 during the first few inches of penetration. This transformation renders the original sectional density irrelevant to the major part of penetrating a game animal. Hunting bullets are designed to do this when they impact at the manufacturer’s prescribed velocities. The result is that penetration depth and expanded diameters are largely independent of the impact velocity for a particular bullet when the velocity is within the manufacturer’s specifications.
We see this by reviewing tests by Gary Sciuchettii which suggest that the penetration depth is indeed largely independent of impact velocity for velocities between 2,000 and 3,000 feet per second. His data is from an extensive test series using effectively all 180 grain 30 caliber bullets available in the mid to late 1990s. Figure C-2 illustrates his results for classic cup and core bullets. These bullets tend to have a small fall off at velocities above about 2700 ft/sec while the more modern design premium and bonded bullets maintain the constant penetration to higher velocities. Partition, Bonded, and all-copper bullets display an even closer approximation of constant penetration depth as velocity reaches and goes slightly above 2000 feet per second.
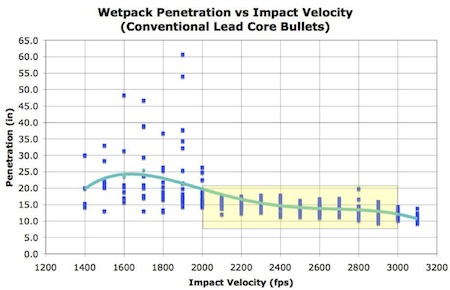
Figure 2. Valid Range for Model is 2000 – 3000 ft/sec. Use manufacturer’s recommended reliable velocity range when available. Image courtesy of rathcoombe.net
How can this be? One way to visualize the underlying cause is to imagine that the bullet plays transformer on impact and penetration into an animal. It starts out as a sleek aerodynamic vehicle that almost immediately changes into a lower density blunt ball-like object generally about twice the diameter of the original bullet. It is this transformed object that does the game-harvesting damage.
Going technical, the theory of strength-dependent hydrodynamic penetration tells us that the bullet erodes moreii with increasing velocity when the pressure on the front end exceeds the bullet’s yield strength. This dynamic shortening is what we see in the first few inches of the penetration event. The remainder of the event is done with an object that kind of looks like a variant of the right-hand side of Figure C-1.
The shortened and expanded bullet makes the actual in-target sectional density more or less inversely proportional to impact velocity. Further, the erosion stops when the pressure drops below the yield point of the bullet material. This inverse relationship between impact velocity and resulting effective sectional density may help explain the Sciuchetti results because penetration depth is generally proportional to the product of velocity and sectional density.
As an aside, brass and copper both have significantly higher yield points than lead. Bullets made from these materials will stop deforming at a higher velocity than lead-core bullets. That higher velocity coupled with more remaining shank at the end of erosion are among the reasons the ‘all-copper’ bullet tends to penetrate so deeply compared to other classes of expanding bullets.
The notion that we get more or less constant penetration depth with increasing velocity appears to be confirmed over a large range of bullet diameters and weights in test data into similar data at rathcoombe.net. Naturally the data is lumped into groups corresponding to bullet construction types because we now know that construction type makes a difference. This constant depth of penetration within the nominal plus or minus 20 per cent scatter is therefore used as a simplifying assumption when moving from 180 grain .30 caliber bullets to other weights and calibers.
Appendix D will show that the depth and final diameters of expanding bullets are mostly functions of the initial weights of hunting bullets impacting within their design velocities.
# # # #
i Sciuchetti, Gary, The Best Hunting Bullet, Handloader, No. 193, pp. 40 – 44, June,1998.
ii Forde, et. al., Symmetric Taylor impact studies of copper, Proc. R. Soc. A (2009) 465, 769–790, November 2008
Navigation Buttons —
| Ideal Weight | Ideal Weight | The Paper | Appendix A | Appendix B | Appendix C | Appendix D |
|---|---|---|---|---|---|---|
| Imperial Units | Metric Units | Defining Ideal Bullet Weight | Math Model | Min. Wound | Depth and Vel. | Depth and Dia. |
 sending...
sending...