Navigation Buttons —
| Ideal Weight | Ideal Weight | The Paper | Appendix A | Appendix B | Appendix C | Appendix D |
|---|---|---|---|---|---|---|
| Imperial Units | Metric Units | Defining Ideal Bullet Weight | Math Model | Min. Wound | Depth and Vel. | Depth and Dia. |
Appendix B. Wound Channel Needed for Rapid Incapacitation
A 1990 paperi by Jan Friis-Hansen published in Antiquity addresses the utility of flint arrowheads used by mesolithic hunters as far back as 10,000 years before the present. The paper used the premise that a successful wound would cause the animal to faint within ten seconds of the injury. This rapid collapse would normally keep the animal from running more than about 100 yards, making recovery of the carcass far more tractable. The author identified the area of the wound channel inside the thoracic cavity as the critical parameter in assessing whether the wound would likely have brought the animal down within the desired time. Another, more recent, paperii at rathcoombe.net cites this work as providing critical insight for the effectiveness of modern hunting bullets. We extend these works to generate a relationship between animal mass and desired minimal thoracic cavity wound channel area for hunting bullets.
Friis-Hansen showed that area of the wound channel defines the rate of blood pressure loss in the brain. He further developed a relationship between animal weight and the size of the wound channel needed to get this rapid blood pressure drop. Figures B-1 and B-2 show how the wound channel area is defined in the Antiquity paper:
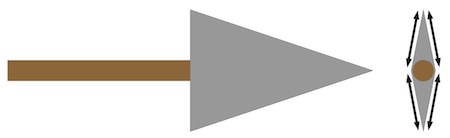
Figure B-1. Arrowhead Perimeter.
The perimeter is indicated by the black lines.
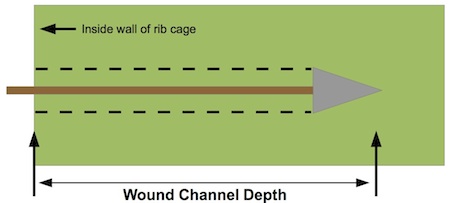
Figure B-2. Depth of wound channel. The critical part of the wound channel lies entirely within the thoracic cavity.
The wound channel area is simply defined as the product of the depth and of the perimeter. A way to visualize this is to think in terms of a hollow tube with an internal shape corresponding to the arrowhead surface. Any arteries, veins or portion of the heart intersecting this tube is presumed to be cut with the rate of internal bleeding or loss of blood pressure established by total area of blood conduit opened.
Note also that the wound channel area is defined by the length of the channel after the chest wall is perforated. The arrow must first pierce this region before it can do the necessary work of cutting arteries, veins, and so on.
The Antiquity paper used anecdotal evidence for two of the three data points used for the fit: the 2,000 lb (900 kg) Caffer (Cape) buffalo and the 45 lb (20 kg) roe deer. The 2,000 lb data point is based on many observations by an experienced hunter. The 45 lb data point was based on arrowhead sizes set by regulatory fiat rather than the smallest size that would bring down the animal within the canonical 10 seconds. In contrast, the 1300 lb (600) kg data point was based on observations of arrows pushed into recently expired beef carcasses with a follow-up detailed examination of the resulting damage.
It is difficult to substantially reduce the time needed for collapse to below ten seconds short of massive trauma or central nervous system disruption. This observation suggests that the wound channel area actually needed to meet the ten second criteria is likely less than the points described in the Antiquity paper, especially for the roe deer. The data is plotted in Figure B-3. Both Friis-Hansen and rathcoombe.net use an approximately linear relationship to represent the trend shown by the three data points.
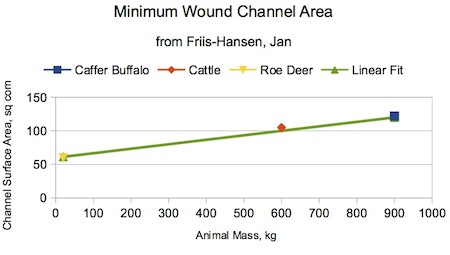
Figure B-3. Minimum Wound Channel Area per Friis-Hansen. Note that the trend would suggest a wound channel area of almost ten square inches (60 sq cm) for a zero-mass animal!
The rathcoombe.net paper represents the relationship with the formula:

The relationship worked well for the objectives of the paper, but leads to nonsensical conclusions for smaller animals. For example, the relationship suggests that a wound channel area of about ten square inches (60 sq cm) is needed to assure that a mouse expires in under ten seconds. It would certainly do that, but a vastly smaller wound would do the same thing. Hence the linear relationship does not appear to properly capture trends for medium game weighing less than about 750 lb (350 kg).
What should the scaling law be? It is clear that the point-slope relationship leads to incorrect results at small weights. Friis-Hansen pointed out that the fraction of blood lost in a particular time should remain the same independent of animal size. This suggests that the ratio of the area opened to the initial blood volume should remain constant. Further, he assumes the volume of blood is approximately proportional to the animal’s mass.
Flow rates are also influenced by pressure, so we need to determine what relationship to use. Thayer Watkinsiii presents a summary of animal mass versus blood pressurethat can be interpreted to suggest that for most mammals, the blood pressure is within about 20% of 125 mm Hg. The exceptions in his data are the very long-necked giraffe and mammals weighing well under the three to four lb (1.5 to 2.0) kg of interest in this discussion. The level of precision in our study suggests that we do not need to explicitly include a blood-pressure term.
These considerations allow us to assume that the required wound channel area is nominally proportional of the cube root of the body mass. We add two data points to better anchor the near-zero trends of the data. The first is based on the author’s personal experience with cottontail rabbits and .22 rimfire CB caps. These nominally 3 lb (1.5) kg rabbits seem to expire well within the 10 seconds when hit in the thoracic cavity with those small rounds. Estimating the thickness within the ribcage to be about 3 inches (~8 cm) yields a wound channel area of 2.2 sq in (14 sq cm) for the .22 cal (~0.5 cm) projectile. The larger 8 lb (3.5 kg) jackrabbit also seems to go down within about 10 seconds for hits in chest regions with .22 cal long rifle ammunition. The wound channel area for this combination is estimated to be about 3 square inches (19 sq cm). We next anchored the high mass region of the curve using the 1300 lb (600 kg) data point provided by Friis-Hansen to generate the power function
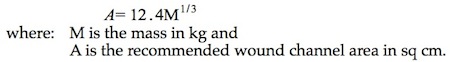
This expression is plotted against the Friis-Hansen and the rabbit data points in Figure B-4:
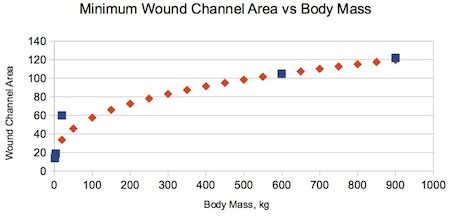
Figure B-4. Power Function Plotted against data. The curve is anchored at zero and by the 1300 lb (600 kg) data points. It passes within 2 percent of the extreme data points and 40 percent of the roe deer data.
# # # #
i Friis-Hansen, Jan, “Mesolithic Cutting Arrows: Functional Analysis of Arrows Used in the Hunting of Large Game”, Antiquity, No. 64, 1990, pp. 494 – 504.
ii http://www.rathcoombe.net/sci-tech/ballistics/wounding.html
iii Watkins, Thayer, http://www.sjsu.edu/faculty/watkins/longevity.htm
Navigation Buttons —
| Ideal Weight | Ideal Weight | The Paper | Appendix A | Appendix B | Appendix C | Appendix D |
|---|---|---|---|---|---|---|
| Imperial Units | Metric Units | Defining Ideal Bullet Weight | Math Model | Min. Wound | Depth and Vel. | Depth and Dia. |
 sending...
sending...